六十年一次的魔法战争就要开始了，大魔法师准备从附近的魔法场中汲取魔法能量。 

大魔法师有 m 个魔法物品，编号分别为 1,2,…,m。每个物品具有一个魔法值，我们用 Xi 表示编号为 i 的物品的魔法值。每个魔法值 Xi 是不超过 n 的正整数，可能有多个物品的魔法值相同。 

大魔法师认为，当且仅当四个编号为 a,b,c,d 的魔法物品满足 Xa < Xb < Xc < Xd , Xb-Xa=2(Xd-Xc)，并且 Xb-Xa<(Xc-Xb)/3 时，这四个魔法物品形成了一个魔法阵，他称这四个魔法物品分别为这个魔法阵的 A 物品，B 物品，C 物品，D 物品。

现在，大魔法师想要知道，对于每个魔法物品，作为某个魔法阵的 A 物品出现的次数，作为 B 物品的次数，作为 C 物品的次数，和作为 D 物品的次数。

第一行包含两个空格隔开的正整数 n,m。 

接下来 m 行，每行一个正整数，第 i+1 行的正整数表示 Xi，即编号为 i 的物品的魔法值。 

保证 1≤n≤15000,1≤m≤40000,1≤Xi≤n。每个 Xi 是分别在合法范围内等概率随机生成的。

共 m 行，每行 4 个整数。第 i 行的 4 个整数依次表示编号为 i 的物品作 为 A,B,C,D 物品分别出现的次数。 

保证标准输出中的每个数都不会超过 10⁹。每行相邻的两个数之间用恰好一个空格隔开。

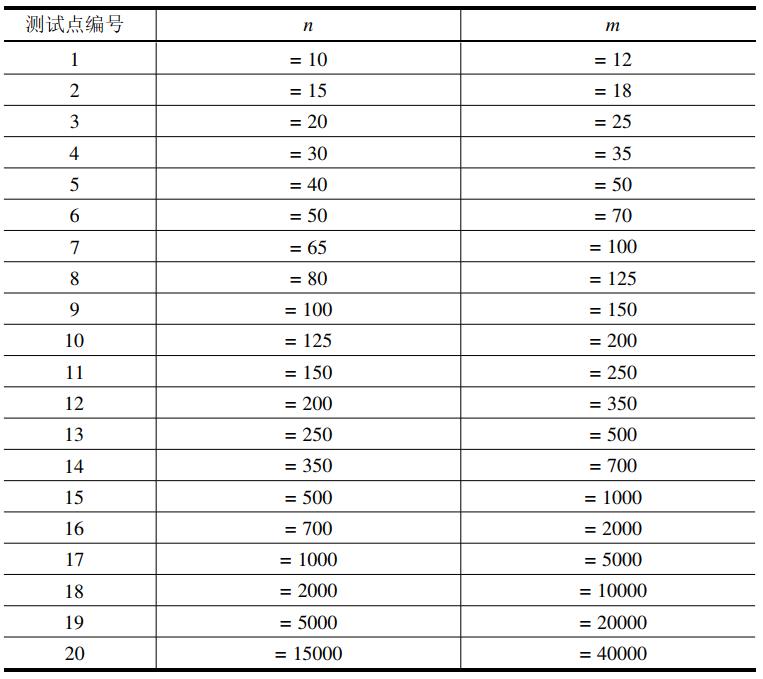
每个测试点的详细数据范围见下表：

【样例解释 1】

共有 5 个魔法阵，分别为：

物品 1,3,7,6，其魔法值分别为 1,7,26,29;

物品 1,5,2,7，其魔法值分别为 1,5,24,26;

物品 1,5,7,4，其魔法值分别为 1,5,26,28;

物品 1,5,8,7，其魔法值分别为 1,5,24,26;

物品 5,3,4,6，其魔法值分别为 5,7,28,29。

以物品 5 为例，它作为 A 物品出现了 1 次，作为 B 物品出现了 3 次，没有作为 C 物品或者 D 物品出现，所以这一行输出的四个数依次为 1,3,0,0。

此外，如果我们将输出看作一个 m 行 4 列的矩阵，那么每一列上的 m 个数之和都应等于魔法阵的总数。所以，如果你的输出不满足这个性质，那么这个输出一定不正确。你可以通过这个性质在一定程度上检查你的输出的正确性。

【样例2输入】

15 15
1 
2 
3 
4 
5
6 
7 
8 
9
10
11
12
13
14
15

【样例2输出】

5 0 0 0
4 0 0 0
3 5 0 0
2 4 0 0
1 3 0 0
0 2 0 0
0 1 0 0
0 0 0 0
0 0 0 0
0 0 1 0
0 0 2 1
0 0 3 2
0 0 4 3
0 0 5 4
0 0 0 5

noip复赛

noip复赛